2.6 Model Checking
In this section, we will learn how to use Cyclone to perform some model checking that uses elementary operators. Essentially, model checking is a technique that can check whether a transition system meets its defined specification. A specification is typically written in a set of Linear Temporal Logic (LTL)/Computational Tree Logic (CTL) formulas.
Though Cyclone's specification language is different from LTL/CTL formulas, one can use some of its features to express the properties described by LTL/CTL formulas.
2-bit Counter
Let us look at a transition system that captures the states of a 2-bit counter. A 2-bit counter has two bits: left (l) and right (r). In order to move from one state to the next one, our 2-bit counter uses the following transition function R:
R: l'= (l ≠ r) ∧ r'=¬r
where l' is a new value for the left bit. This value is computed based on the values from l and r in the previous state. Similarly, r is calculated by negating its value in previous state. Hence, based on this transition function R we now can plot the following state chart.
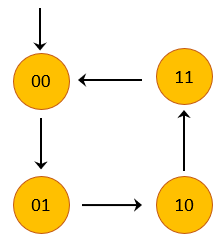
The initial state set both l and r to 0 (false) by using the following LTL formula:
¬l ∧ ¬r
Now suppose we want to check the following property:
Property: G(¬l ∨ ¬ r)
G here is a temporal operator and represents globally (◻). Thus, this property states that either left or right bit is not set and this should be always true in our transition system.
One can use a traditional model checker (such as NuSMV) to check the above property. Since a transition system is really just a graph, Cyclone can also be used for model checking in a very unique way.
Now, let us show you how to use Cyclone to model check this transition system against our property.
First, we define how left and right bit changes based on our transition function in a single state S:
normal start state S {
l = (l!=r);
r = !r;
}
Next, we create a transition. In this case, we can just simply loop on our state S since transition function is defined inside S.
trans t { S -> S }
How do we express our temporal property ? In previous sections, we used invariant statement to express a formula/property must hold in all states. That is no matter which execution path Cyclone explores, an invariant must hold. Thus, we can use an invariant to express G operator.
invariant property { (!l || !r); }
Finally, we would like to say that at initial state l and r are both set to 0. In Cyclone, you could use an initial statement to specify an initial condition for a variable. If a variable is used with an initial statement, then it refers to the initial state. A state even before defined start state.
assert ( !initial(l) && !initial(r) );
Recall that if a specification contains an invariant, Cyclone will look for a counter-example that can break the invariant. Thus, we use the following statement to model check whether this specification satisfies our property.
check for 2,3,4 reach(S)
In fact, we ask Cyclone to perform bounded checking for the execution paths that have a length of 2, 3 and 4 respectively. In this case, Cyclone successful finds a counter-example with an execution path length of 3. Hence, our property does not hold for this specification.
Alternatively, one can simply just use an assert to express our property instead of an invariant.
assert !(!l || !r);
Here, we are asking Cyclone to discover an execution path that make our property failed. It is equivalent to the LTL formula:◇ !property
Note that a smaller bound may unable to reveal a design flaw. In this sense, multiple different larger bounds can be used just like the ones we used. The full specification is available here.
A Transition System
Given a transition system as follows, sometime we would like to find a path such that a set of propositions always hold. In this scenario, we could use always modifier in an assert statement.
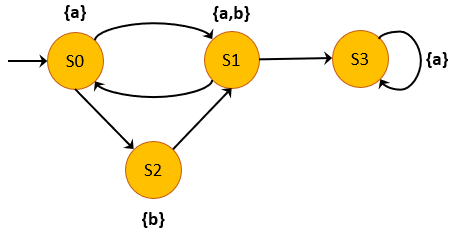
In this transition system, L(S0)=L(S3)={a}, L(S1)={a,b} and L(S2)={b}. Suppose we would like check the following property:
Property: there exists a path that a always holds.
Surely, one can use an invariant to check whether there exists a path that a does not hold. We can simply enumerate all possible such paths, and whatever remains must be the path satisfies our property. However, this approach is not natural and quite tedious. To facilitate such scenario, Cyclone provides a keyword always that can be used with along with an assert statement. They keyword always tells Cyclone a boolean expression must hold at all times. Therefore, we can use the following statement to express our property:
assert always ( a );
This tells Cyclone to find a path that a always holds. In this transition system, path S0 -> S1 -> S3 -> S3 -> ... satisfies this property. The above assert statement acts like ∃◻ in CTL (Computation Tree Logic). Similarly, the following assert statement acts like ∃◇.
assert some ( a );
Note the difference between an assert statement without using keyword some and a one with some is as follows:
- assert ( a ): Finds a path that leads to a holds. a only needs to hold when a path is terminated/a state is reached.
- assert some ( a ): Finds a path that a holds sometime in a path. Thus, a may not hold when a path is terminated/a state is reached.
Execution Result
Press 'run' to execute the code and see checking results.
Execution server didn't supply any information
URL: /server