2.8 Exercises (2)

Analyzing Recursive Functions

The McCarthy91 function is a recursive function. It is often used as a test case for formal verification within computer science. The McCarthy91 function is defined as follows:

• Use Cyclone to model this recursive function and show that M(87)=91.
• Use Cyclone to prove that for any n ≤ 100, M(n) always returns 91. You may assume that the upper bound here is 200 steps (check for 200).

Hint: you need to use an additional variable s to remember the number of function calls on a stack. When s is zero, M(n) should have its results based on the definition above.

Dijkstra's Token Ring Algorithm

One of the most famous algorithms in distributed system is Dijktra's token ring algorithm. This algorithm has started the self-stabilization field as a subfield of fault-tolerance. It still receives interest even after 40 years.

So what is self-stabilization ? If you haven't heard the term before, no worries. We explain the term here. Let's put it in a simple way. Regardless of a system's initial state, a self-stabilization algorithm can ensure a system to converge to a legitimate state within a bounded amount of time without any outside intervention.

Dijkstra describes his ring token algorithm originally in this paper. So how does this algorithm work ? There are some machines connected in a ring fashion (see the following picture) and

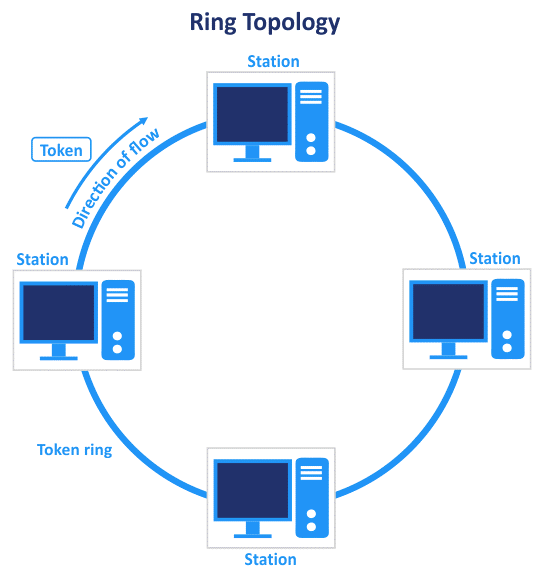
each of them needs a token to have access to some resources. The invariant here is that there is exactly one token in the ring. Hence, there is exactly one machine can have access to the resources. This is what we called the stable state. So what are the bad states. There are two cases here:

• 1. There are no tokens in a ring.
• 2. There are more than one tokens in a ring.

To deal with these two cases, Dijkstra uses the following code:

For the first machine: if L=S then S=(S+1) mod k

For the other machines: if L≠S then S=L

So the L here represents the state of current machine, S here is state of the next machine in the ring. k here means the number of states of a machine could have. If the state of current machine (L) is not equal to the state of next machine (S), then L has the token. However, when the state of the first machine is equal to the last machine in the ring, then this means that L has the token. For example, suppose we only use a two-state variable for each machine. Then, the following configuration represent:

• 1100 (machine 1 has the token.)
• 1011 (machine 1,2 and 0 has the token, respectively.)
• 0101 (machine 1,2 and 3 has the token, respectively.)

You may model this algorithm in some other specification language such as TLA+, then model check all possible states of this algorithm could have.

However, our ring here is really just a graph and each machine in this ring is a node. Hence, using a graph-based specification might be much more natural to model this algorithm. We can use Cyclone to show this algorithm is self stabilizing in a very unique way. We may also use Cyclone to observe how this algorithm eventually converges to a stable state (given any initial states) by producing a trace.

Suppose we have a total of 4 machines and each machine has 5 different states. Now use Cyclone to model this scenario and show/prove that this algorithm is self stabilizing.

Hint: you may add option-trace=true; at the beginning of your spec to ask Cyclone to produce a trace. A trace in Cyclone is a sequence of states (nodes) that contain concrete values for each variable (used for computation). Thus, in this way you can observe how a system starting from a bad state converges to the stable state.